Ebben a cikkben azt fogjuk górcső alá venni, hogy miként is lehet Excel segítségével korrelációs mátrixot készíteni, hiszen gyakran előfordulhat olyan eset a munkánk során, hogy szükségünk lenne az egyes változók között fennálló kapcsolat milyenségét és irányát leíró információra, azonban hirtelen nem áll rendelkezésünkre statisztikai elemző eszköz, csak az Excel.
Mielőtt azonban rátérnénk a gyakorlati megvalósításra, mindenképpen szükséges néhány szót ejteni a korreláció elméleti hátteréről is.
A korrelációt mennyiségi ismérvek közötti sztochasztikus kapcsolatként értelmezzük, ahol a vizsgált változókról feltételezzük a linearitást. A kapcsolat irányáról, illetve szorosságáról a lineáris korrelációs együttható (vagy más néven Pearson-féle korrelációs együttható – jele: rx,y) segítségével kapunk információt, melynek értéke +1 és -1 közé esik.
A kapcsolat szorosságának egy lehetséges értelmezése:
|rx,y| = 0,00 → a kapcsolat hiánya
0,01 ≤ |rx,y| ≤ 0,30 → a kapcsolat gyenge
0,31 ≤ |rx,y| ≤ 0,49 → a kapcsolat közepesnél gyengébb
|rx,y| ≅ 0,50 → a kapcsolat közepes
0,51 ≤ |rx,y| ≤ 0,80 → a kapcsolat közepesnél erősebb
0,81 ≤ |rx,y| ≤ 0,99 → a kapcsolat erős
|rx,y| = 1,00 → a kapcsolat függvényszerű
Mindenképpen szükséges megjegyezni, hogy a korreláció segítségével az egyes változók együttmozgásáról kaphatunk képet, nem pedig az ok-okozati összefüggésről.
Az elméleti áttekintést követően tekintsünk át egy egyszerű példát.
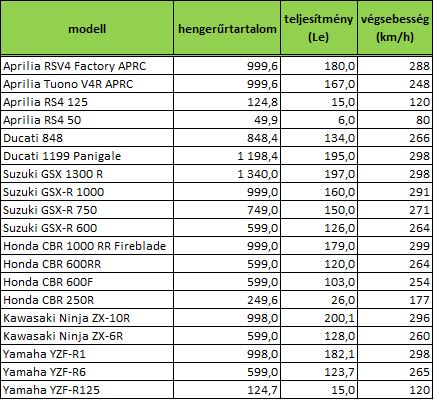
Racings Kft. motorokkal kapcsolatban készít kutatást, amelyben leginkább arra kíváncsi, hogy milyen összefüggés áll fent a motor hengerűrtartalma, lóereje, illetve végsebessége között.
A vizsgálathoz szükséges alapadatok:
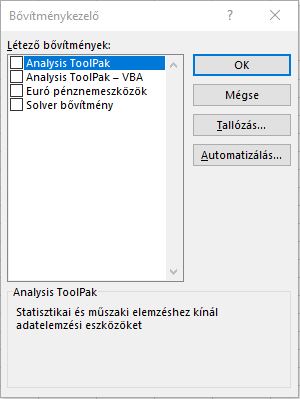
A korrelációs mátrix elkészítéséhez az Excel Adatelemzés funkcióját fogjuk használni, melyet, ha még ezt korábban nem tettük volna meg, a Fájl/Beállítások lehetőségen belül a Bővítmények fülön tudjuk beállítani. A Kezelés részen válasszuk ki az Excel-bővítmények lehetőséget, majd kattintsunk az Ugrás... gombra. Ekkor felugrik egy ablak, ahol alapvetően négy lehetőség közül választhatunk.
Válasszuk ki az Analysis ToolPak-et, majd kattintsunk az OK gombra.
Ennek hatására az Adatok szalagon megjelenik az Elemzés panel, mely már tartalmazza a szükséges Adatelemzés menüpontot.
A korrelációs mátrix létrehozásához hívjuk is be az említett új funkciót, ahol válasszuk ki a Korrelációanalízis lehetőséget.
A Bemeneti tartomány részhez hivatkozzuk be a vizsgálandó numerikus változóinkat. Mivel az adataink oszlopokban kerültek letárolásra, válasszuk az Oszlopok csoportosítási alapot, és amennyiben a kijelölés tartalmazza az oszlopfejlécet, kattintsuk be a Feliratok az első sorban jelölőnégyzetet egyaránt.
Lehetőségünk van továbbá megadni, hogy az eredmények hol kerüljenek megjelenítésre. Most válasszuk az Új munkalapra opciót, majd kattintsunk az OK gombra, melynek hatására egy új munkalapon megjelenik a korrelációs mátrix.
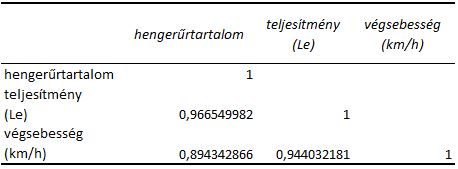
A mátrix a vizsgált változók közötti korreláció irányát és szorosságát páronként szemlélteti, s látható továbbá az is, hogy a főátlóban végig egy szerepel, hiszen itt az adott változó önmagával való korrelációját lehet leolvasni, ami nyilvánvalóan függvényszerű.
A kapott eredmények alapján jól látható, hogy mindhárom változó között páronként pozitív irányú erős kapcsolat áll fent.
Amennyiben ennél tovább megyünk az értelmezést illetően, fontos szem előtt tartani, hogy csak akkor bocsátkozzunk komolyabb következtetések levonására, amennyiben megfelelő szakismerettel rendelkezünk az adott témát illetően, és ismerjük a változók közötti ok-okozati viszonyokat.
Vegyük példaként a teljesítmény és végsebesség párost. Nagy valószínűséggel nem követünk el nagy hibát, ha azt feltételezzük, hogy a nagyobb teljesítményhez nagyobb végsebesség is párosul, s ebből ered a pozitív irányú erős kapcsolat.